Contents

Integrating Learning and Planning

Integrating Learning and Planning

Warning

Please note that this notebook is still work in progress, hence some sections could behave unexpectedly, or provide incorrect information.

The goal of this lecture is to provide as an introduction of learning a model of an MDP directly from experience, and use planning to construct a value function or policy. These two are then combined into a single architecture. The difference between Model-Free and Model-Based RL are the following:

  • Model-Free

    No model, learn value function (and/or policy) from experience

  • Model-Based

    Learn model from experience, plan value function (and/or policy) from model

Model-Based RL

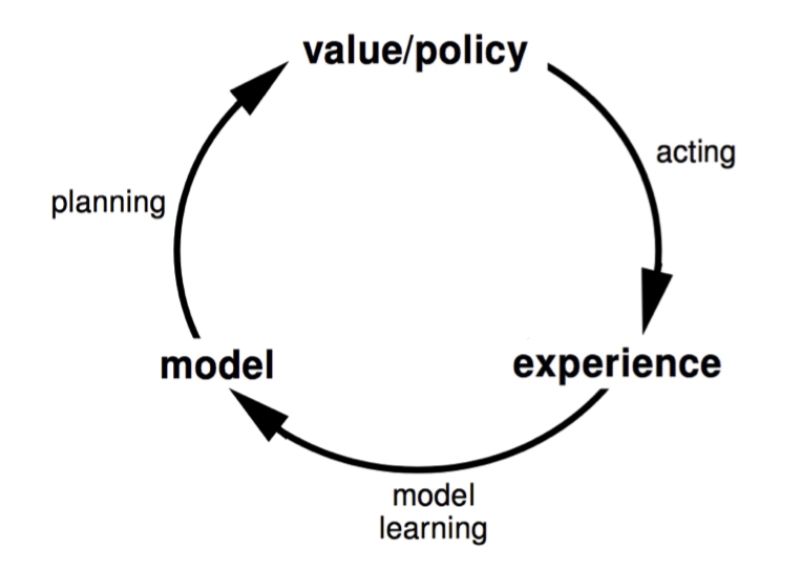
../../_images/model-based-rl.png

Fig. 7 The model-based reinforcement learning cycle

The advantages of Model-Based RL are that models can be efficiently learned using supervised learning methods. It is also possible to then reason of model uncertainty. A disadvantage, however, is that first the model must be learned. Only then can the value function be constructed. This also means there are two sources of approximation error, and the accuracy of the value function is limited to the accuracy of the model.

A model \(M\) is a representation of an MDP parameterized by \(\eta\). In this case, it is assumed that the state and action spaces are known (for simplification). So then, a model \(M = (P_\eta, R_\eta)\) represents state transitions \(P_\eta \approx P\) and rewards \(R_\eta = R\). These can be used to estimate rewards and state transitions:

\[\begin{split} S_{t+1} & \sim P_\eta(S_{t+1} | S_t, A_t)\\ R_{t+1} & = R_\eta(S_{t+1} | R_t, A_t)\end{split}\]

Typically, a conditional independence between state transitions and rewards are assumed (\(P(S_{t+1}, R_{t+1} | S_t, A_t) = P(S_{t+1} | S_t, A_t)P(R_{t+1} | S_t, A_t)\)).

So, the goal is to estimate \(M_\eta\) from experience \(\{S_1, A_1, R_2, ..., S_T\}\). This is a supervised learning problem. More specifically, it is usually best to split up the two tasks of learning \(R_\eta\) and \(P_\eta\). \(S_t, A_t \Rightarrow R_{t+1}\) is a regression problem, while \(S_t, A_t \Rightarrow S_{t+1}\) is a density estimation problem.

There are a lot of ways to create a model. This chapter focusses on the Table-Lookup Model.

Table-Lookup Model

The idea here is to count the visits \(N(s, a)\) to each state-action pair. Then, similar to what TD learns, the idea is to construct the maximum-likelihood Markov model from this. It can be constructed in the following manner.

(5)\[\begin{split} & \hat{P^a_{ss'}} = \frac{1}{N(s,a)} \sum_{k = 1}^K \sum_{t = 1}^{T_k} 1(s^k_t, a^k_t, s^k_{t+1} = s, a, s')\\ & \hat{R^a_{s}} = \frac{1}{N(s,a)} \sum_{k = 1}^K \sum_{t = 1}^{T_k} 1(s^k_t, a^k_t = s, a)r^k_t\end{split}\]

Alternative, it is possible to record an experience tuple \((S_t, A_t, R_{t+1}, S_{t+1})\) at each time-step \(t\). In order to then sample the model, uniformly randomly pick a tuple matching \((S_t, A_t, ., .)\).

Planning with a Model

Given a model \(M_\eta = (P_\eta, R_\eta)\), the goal is to solve the MDP \((S, A, P_\eta, R_\eta)\) using a planning algorithm (e.g. Value iteration, Policy iteration, Tree search, …).

Algorithms like Value iteration are quite expensive, since they go over the entire state(-action) space. Sample-Based planning uses the model to generate samples. This is often much more efficient. It also means more frequent states will be sampled more often. This can be a good property to have.

The sampling happens in the same way as in equation (5). At each step, model-free RL can be applied to the samples (e.g. Monte-Carlo control, SARSA, Q-Learning, …).

Given an imperfect model \((P_\eta, R_\eta) \neq (P, R)\), the performance of model-based RL is limited to the optimal policy of approximate MDP \((S, A, P_\eta, R_\eta)\). So, when the model is inaccurate, planning will compute a sub-optimal policy. It is always possible to switch to model-free RL. However, there are ways of reasoning about the uncertainty in the model. This can be done using for example Bayesian modelling.

Integrated Architectures

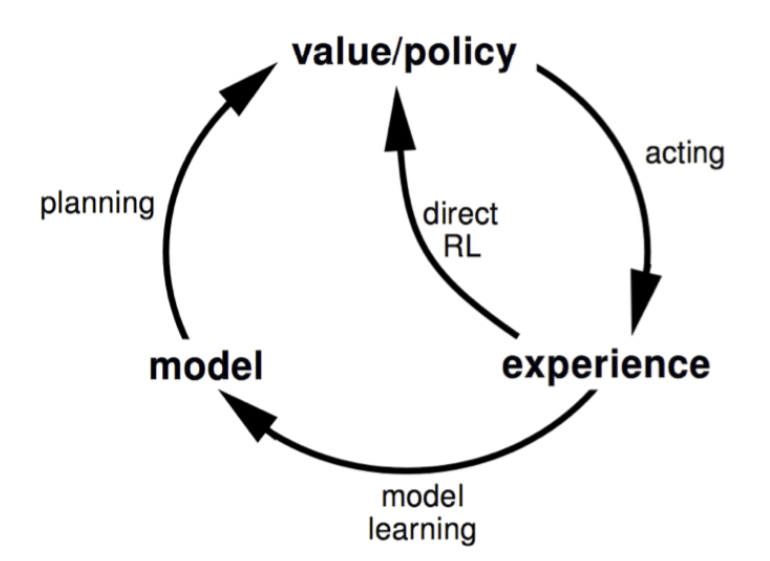
../../_images/dyna.png

Fig. 8 Dyna architecture cycle

It is possible to learn and plan the value function (and/or policy) from real and simulated experience. This architecture is referred to as Dyna.The algorithm below uses Dyna with Q-Learning.

            \begin{algorithm}
	\caption{Dyna-Q}
	\begin{algorithmic}
		\REQUIRE $Q$, $M$, $n$ (number of planning steps)
		\STATE $S \Leftarrow$ current state
		\STATE $A \Leftarrow \epsilon$-greedy($S, Q$)
		\STATE Execute $A$; observe $R, S'$
		\STATE $Q(S, A) \Leftarrow Q(S, A) + \alpha \left[R + \gamma \max_a Q(S', a) - Q(S, A)\right]$
		\STATE $M \Leftarrow R,S'$
		\FOR{$i = 1,...,n$}
			\STATE $S, A \Leftarrow$ random previously taken state-action pair
			\STATE $R, S' \Leftarrow M(S, A)$
			\STATE $Q(S, A) \Leftarrow Q(S, A) + \alpha \left[R + \gamma \max_a Q(S', a) - Q(S, A)\right]$
		\ENDFOR
	\end{algorithmic}
\end{algorithm}

Here, the Q-function is learned from both real experience and planned experience.

previous

Model-Free Control

next

Exploration and Exploitation