This is my first official group project, which was completed in Fall 2020 for the Project 1-1 course at my bachelor’s Data Science and Artificial Intelligence at Maastricht University.

Phase 1: The 2-Dimensional Knapsack Problem

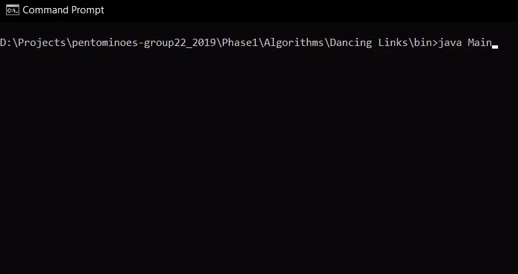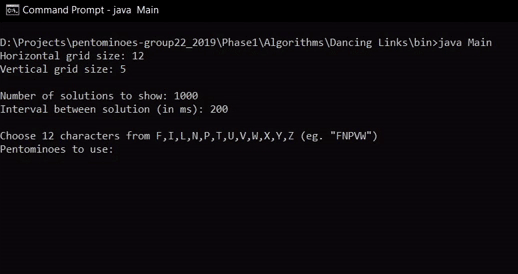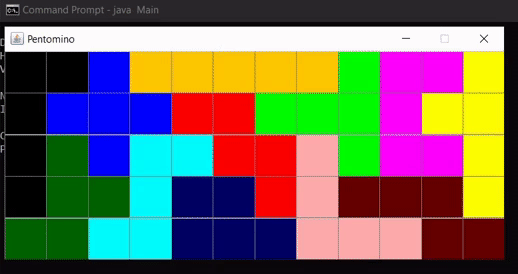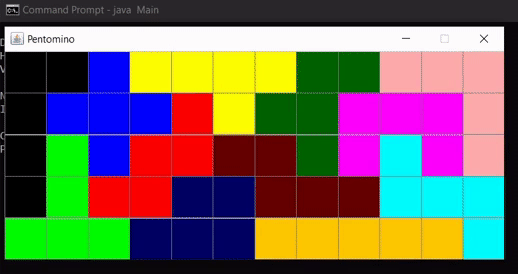
Initially, we focussed on the 2-dimensional knapsack problem. Given the shapes of pentominoes, the goal was to see if they could be used to create a perfect fit on a grid of any size. We implemented the dancing links algorithm, invented by Donald Knuth, to do efficient planning for this problem. The result is shown in the GIF below.

The GIF above displays examples of the results of the algorithm for a certain configuration.

Phase 2: Pentris

In the second phase of the project we decided to learn about different planning algorithms and genetic algorithms to learn how to play a game of Tetris with pentominoes! We also learned how to use JavaFX, save and load high scores, and even include music in the game. You can see the final product on the left!

Phase 3: Optimizing for the Bounded 3D Knapsack Problem

Finally, we decided to apply our knowledge from the previous two phases in order to develop software that is able to optimally pack parcels into a 3-dimensional container. We developed 6 types of parcels of different sizes, for which the user is able to fill in their amounts and values. The goal of the algorithm is to fill the container with parcels such that the cumulative value is maximized. We used genetic algorithms and modified the 2-dimensional version of the dancing links algorithm to 3-dimensional space, and made it work with incomplete solutions. The final result can be seen in the video below!

The solution to an example configuration being showcased for the final product.

The final report for this project is attached below!